| 求圆周率π一万位程序分析 | 您所在的位置:网站首页 › bbp公式计算pi的第n位 十进制 › 求圆周率π一万位程序分析 |
求圆周率π一万位程序分析
|
先贴一段维基百科的内容: 计算机时代计算π上万位以上的小数位值通常利用高斯-勒让德算法或波温算法;另外以往亦曾使用于1976年发现的萨拉明-布伦特算法。 第一个π和1/π的小数点后首一百万位利用了古腾堡计划。最新纪录是2002年9月得出的1,241,100,000,000个小数位,由拥有1TB主内存的64-node日立超级计算机,以每秒200亿运算速度得出,比旧纪录多算出一倍(206亿小数位)。此纪录由以下梅钦类公式得出: 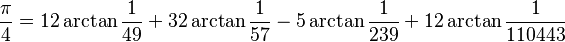 (K. Takano, 1982年) (K. Takano, 1982年) (F. C. W. Störmer, 1896年) (F. C. W. Störmer, 1896年)
这么多的小数位没什么实用价值,只用以测试超级计算机。 1996年,David H. Bailey、Peter Borwein及西蒙·普劳夫发现了π的其中一个无穷级数: 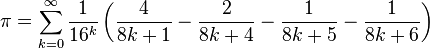
以上述公式可以计算π的第n个二进制或十六进制小数,而不需先计算首n-1个小数位。此类π算法称为贝利-波尔温-普劳夫公式。请参考Bailey's website 上相关程式。 法布里斯·贝拉于1997年给出了计算机效率上高出上式47%的BBP算法: 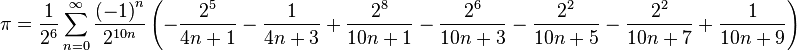
请参考Fabrice Bellard's PI page 。 其他计算圆周率的公式包括:  (拉马努金Ramanujan) (拉马努金Ramanujan)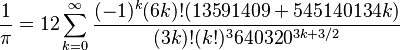 (David Chudnovsky及Gregory Chudnovsky) (David Chudnovsky及Gregory Chudnovsky)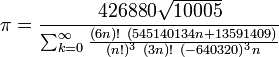 [2] [2]
编写计算机程序时,也可以利用反三角函数直接定义  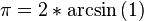
利用余弦函数   几何
若圆的半径为r,则其周长为C = 2πr若圆的半径为r,则其面积为S =πr2若椭圆的长、短两轴分别为a 和 b ,则其面积为S = πab若球体的半径为 r,则其体积为 V = (4/3)πr3若球体的半径为r,则其表面积为 S = 4πr2角:180度相等于π弧度
几何
若圆的半径为r,则其周长为C = 2πr若圆的半径为r,则其面积为S =πr2若椭圆的长、短两轴分别为a 和 b ,则其面积为S = πab若球体的半径为 r,则其体积为 V = (4/3)πr3若球体的半径为r,则其表面积为 S = 4πr2角:180度相等于π弧度
环面的体积和表面积公式  
R是管子的中心到画面的中心的距离, r是圆管的半径。 [编辑]代数π是个无理数,即不可表达成两个整数之比,是由Johann Heinrich Lambert于1761年证明的。 1882年,Ferdinand Lindemann更证明了π是超越数,即不可能是任何有理数多项式的根。 圆周率的超越性否定了化圆为方这古老尺规作图问题的可能性,因所有尺规作图只能得出代数数,而超越数不是代数数。 [编辑]数学分析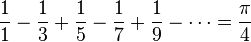 (Leibniz定理) (Leibniz定理) (Wallis乘积) (Wallis乘积)  (由欧拉证明,参见巴塞尔问题) (由欧拉证明,参见巴塞尔问题)
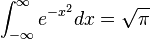 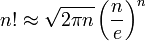 (斯特林公式) (斯特林公式)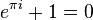 (欧拉公式) (欧拉公式)
π有个特别的连分数表示式: 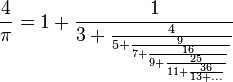
π本身的连分数表示式(简写)为[3;7,15,1,292,1,1,1,2,1,3,1,14,2,1,1,2,...],其近似部分给出的首三个渐近分数  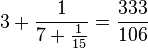 
第一个和第三个渐近分数即为约率和密率的值。数学上可以证明,这样得到的渐近分数,在分子或分母小于下一个渐进分数的分数中,其值是最接近精确值的近似值。 (另有12个表达式见于[3] ) [编辑]数论 两个任意自然数是互质的概率是 。任取一个任意整数,该整数没有重复质因子的概率为 。任取一个任意整数,该整数没有重复质因子的概率为 。一个任意整数平均可用 。一个任意整数平均可用 个方法写成两个完全数之和。
[编辑]概率论
取一枚长度为l的针,再取一张白纸在上面画上一些距离为2l的平行线。把针从一定高度释放,让其自由落体到纸面上。针与平行线相交的概率是圆周率的倒数(泊松针)。曾经有人以此方法来寻找π的值。
[编辑]动态系统/遍历理论 个方法写成两个完全数之和。
[编辑]概率论
取一枚长度为l的针,再取一张白纸在上面画上一些距离为2l的平行线。把针从一定高度释放,让其自由落体到纸面上。针与平行线相交的概率是圆周率的倒数(泊松针)。曾经有人以此方法来寻找π的值。
[编辑]动态系统/遍历理论
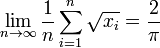 对[0, 1]中几乎所有x0,其中 xi是对于r=4的逻辑图像迭代数列。
[编辑]物理学 对[0, 1]中几乎所有x0,其中 xi是对于r=4的逻辑图像迭代数列。
[编辑]物理学
 (此为常态分配的机率密度函数) (此为常态分配的机率密度函数)
求圆周率π的C程序分析
long a=10000, b, c=2800, d, e, f[2801], g;main(){ for(;b-c;) f[b++]=a/5;for(;d=0,g=c*2;c-=14,printf("%.4d",e+d/a),e=d%a)for(b=c; d+=f[b]*a, f[b]=d%--g, d/=g--, --b; d*=b); scanf("%s");} 简短的4行代码,就可以精确计算机出800位的PI(圆周率)值。实在太震撼人心了。这样的程序也能运行,竟然还能能完成这样让人难以置信的任务,真是太神了。 一、源程序本文分析下面这个很流行的计算PI的小程序。下面这个程序初看起来似乎摸不到头脑,不过不用担心,当你读完本文的时候就能够基本读懂它了。程序一:很牛的计算Pi的程序#include int a=10000,b,c=2800,d,e,f[2801],g; main(){for(;b-c;) f[b++]=a/5;for(;d=0,g=c*2;c -=14,printf("%.4d",e+d/a),e=d%a) for(b=c; d+=f[b]*a,f[b]=d%--g,d/=g--,--b; d*=b);} 二、数学公式数学家们研究了数不清的方法来计算PI,这个程序所用的公式如下: pi = 2 + 1/3 * (2 + 2/5 * (2 + 3/7 * (2 + ... (2 + k/2k+1 * (2 + ... ))...))) 至于这个公式为什么能够计算出PI,已经超出了本文的能力范围。下面要做的事情就是要分析清楚程序是如何实现这个公式的。我们先来验证一下这个公式:程序二:Pi公式验证程序#include void main(){ float pi=2; int i; for(i=100;i>=1;i--) pi=pi*(float)i/(2*i+1)+2; printf("%f\n",pi); getchar();}上面这个程序的结果是3.141593。 三、程序展开在正式分析程序之前,我们需要对程序一进行一下展开。我们可以看出程序一都是使用for循环来完成计算的,这样做虽然可以使得程序短小,但是却很难读懂。根据for循环的运行顺序,我们可以把它展开为如下while循环的程序: 程序三:for转换为while之后的程序#include int a=10000,b,c=2800,d,e,f[2801],g;main() {int i;for(i=0;i long b, c=2800, d, e, f[2801]; main(){ while(b-c!=0){ f[b]=2000; b++; } while(c!=0){ b=c; d=f[b]*10000; f[b]=d%(b*2-1); d=d/(b*2-1); --b; while(b!=0){ d=d*b+f[b]*10000; f[b]=d%(b*2-1); d=d/(b*2-1); --b; } c-=14; printf("%.4d",e+d/10000); e=d%10000; } } 少了两个变量了! 深入分析 好了,马上进入实质性的分析了。一定的数学知识是非常有必要的。首先,必须知道下面的公式可以用来求pi: pi/2=1+1!/3!!+2!/5!!+3!/7!!+...+k!/(2*k+1)!!+...(注:双阶乘 双阶乘m!!表示: 当m是自然数时,表示不超过m且与m有相同奇偶性的所有正整数的乘积。如:3!!=1*3=3,6!!=2*4*6=48(另0!!=1) 当m是负奇数时,表示绝对值小于它的绝对值的所有负奇数的绝对值积的倒数。如:(-7)!!=1/(|-5| * |-3| * |-1|)=1/15 当m是负偶数时,m!!。 (2n-1)!!=1*3*5*7......(2n-1)(2n)!!=2*4*6*8...........(2n)比如7!!=1*3*5*78!!=2*4*6*8) 只要项数足够多,pi就有足够的精度。至于为什么,我们留给数学家们来解决。 写过高精度除法程序的人都知道如何用整数数组来进行除法用法,而避免小数。其实很简单,回想一下你是如何徒手做除法的。用除数除以被除数,把得数放入结果中,余数乘以10后继续做下一步除法,直到余数是零或达到了要求的位数。 原程序使用的数学知识就那么多,之所以复杂难懂是因为它把算法非常巧妙地放到循环中去了。我们开始具体来分析程序。首先,我们从数学公式开始下手。我们求的是pi,而公式给出的是pi/2。所以,我们把公式两边同时乘以2得: pi=2*1+2*1!/3!!+2*2!/5!!+2*3!/7!!+...+2*k!/(2*k+1)!!+... 接着,我们把它改写成另一种形式,并展开: pi=2*1+2*1!/3!!+2*2!/5!!+2*3!/7!!+...+2*n!/(2*n+1)!! =2*(n-1)/(2*n-1)*(n-2)/(2*n-3)*(n-3)/(2*n-5)*...*3/7*2/5*1/3 +2*(n-2)/(2*n-3)*(n-3)/(2*n-5)*...*3/7*2/5*1/3 +2*(n-3)/(2*n-5)*...*3/7*2/5*1/3 +2*3/7*2/5*1/3 +2*2/5*1/3 +2*1/3 +2*1对着公式看看程序,可以看出,b对应公式中的n,2*b-1对应2*n-1。b是从2800开始的,也就是说n=2800。(至于为什么n=2800时,能保证pi的前800位准确不在此讨论范围。)看程序中的相应部分: d=d*b+f[b]*10000;f[b]=d%(b*2-1);d=d/(b*2-1); d用来存放除法结果的整数部分,它是累加的,所以最后的d将是我们要的整数部分。而f[b]用来存放计算到b为止的余数部分。 到这里你可能还不明白。一是,为什么数组有2801个元素?很简单,因为作者想利用f[1]~f[2800],而C语言的数组下标又是从0开始的,f[0]是用不到的。二是,为什么要把数组元素除了f[2800]都初始化为2000?10000有什么作用?这倒很有意思。因为从printf("%.4d",e+d/10000); 看出d/10000是取d的第4位以前的数字,而e=d%10000; ,e是d的后4位数字。而且,e和d差着一次循环。所以打印的结果恰好就是我们想要的pi的相应的某4位!开始时之所以把数组元素初始化为2000,是因为把pi放大1000倍才能保证整数部分有4位,而那个2就是我们公式中两边乘的2!所以是2000!注意,余数也要相应乘以10000而不是10!f[2800]之所以要为0是因为第一次乘的是n-1也就是2799而不是2800!每计算出4位,c都要相应减去 14,也就保证了一共能够打印出4*2800/14=800位。但是,这竟然不会影响结果的准确度!本人数学功底不高,无法给出确切答案。(要是哪位达人知道,请发email到[email protected]告诉我哦。) 偶然在网上见到一个根据上面的程序改写的“准确”(这个准确是指没有漏掉f[]数组中的的任何一个元素。)打印2800位的程序,如下: long b,c=2800,d,e,f[2801],g;int main(int argc,char* argv[]){ for(b=0;b f[b] = 2; e=0; while(c > 0) { d=0; for(b=c;b>0;b--) { d*=b; d+=f[b]*10; f[b]=d%(b*2-1); d/=(b*2-1); } c-=1; printf("%d",(e+d/10)%10); e=d%10; } return 0;} 不妨试试把上面的程序压缩成3行。 我稀里糊涂算是看完了,但是对那个计算π的公式还是没有推出来。我翻了一下高数课本,找了一下arcsin和 如果让x=1,可以得到arccos1 = 0 = =π/2-∑[(2k)!/((2k+1)(2^k*k!))]x^(2k+1)(k=0,1,2,3,4.....),所以 π/2 = ∑[(2k)!/((2k+1)(2^k*k!))]x^(2k+1)(k=0,1,2,3,4.....),但是和给的公式不一样,不知道那个是怎么推出来的。 |
【本文地址】
 值,但是编译器必须具备三角函数的函式库:利用正弦函数
值,但是编译器必须具备三角函数的函式库:利用正弦函数 (海森堡不确定性原理)
(海森堡不确定性原理)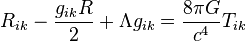 (相对论的场方程)
(相对论的场方程) arccos的幂级数公式
arccos的幂级数公式